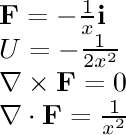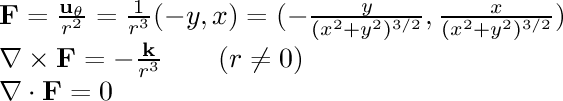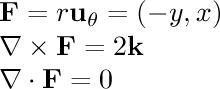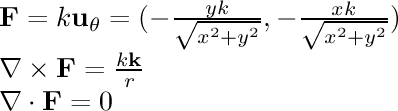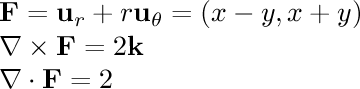Click here to go to the applet.
This applet demonstrates various properties of
vector fields.
You can select from a number of vector fields and see how
particles move if it is treated as either a velocity
or a force field. This helps you visualize the field.
When you start the applet, you will see 500 particles moving in the
"1/r^2 single" field, which is a field that attracts
particles to the center. By default the
particles are treating the field as a velocity field, which means
that the field vectors determine how fast the particles are moving and in
what direction. In this case, the particles just move toward the center.
The velocity of all the particles at a certain point
on the grid is always the same. If the field is a force field, then the
field vectors determine the acceleration of the particles, but their velocity
may vary depending on where they started.
The Field Selection popup will allow you to select a
vector field. The choices are:
- 1/r^2 single:
This field is associated with gravity and electrostatic attraction.
The gravitational field around a planet and the electric field
around a single point charge are similar to this field.
The field points towards the origin and is inversely proportional
to the square of the distance from the origin.
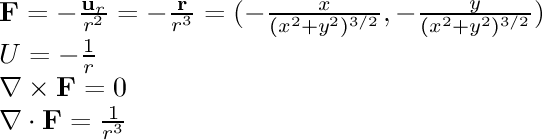
- 1/r^2 double:
This field is associated with gravity and electrostatic attraction.
The gravitational field around two planets and the electric field
around two negative point charges are similar to this field.
The separation of the two centers is adjustable.
- 1/r single line:
This field is associated with electrostatic attraction.
If we calculate the electric field around an infinitely long conductor
in a straight line with a uniform charge along its length, we find that
the field strength is
inversely related to the distance from the line.
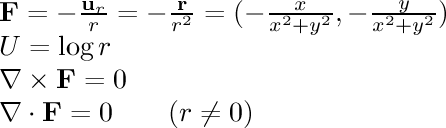
- 1/r double lines:
This is the field around two infinitely long conductors. The distance
between them is adjustable.
- 1/r rotational:
In this field, the particle is being pulled in a circle around the
center line. The speed of its motion is inversely proportional to its
distance from the line.
If we calculate the magnetic field around an infinitely long conductor
in a straight line with a uniform current along its length, we find that
the field strength is
inversely related to the distance from the line.
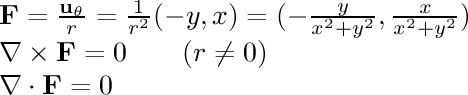
- 1/r rotational double:
Here we have two centers of rotation, with an adjustable distance
between them.
- 1/r rotational double + ext:
Same as above, but a constant external field is added in.
The strength and angle of the external field is adjustable.
- 1/r rotational dipole:
Here we have two centers of rotation, with rotation in
opposite directions, with an adjustable distance between them.
- 1/r rotational dipole + ext:
Same as above, but a constant external field is added in.
The strength and angle of the external field is adjustable.
(In fluid dynamics this field is called the
Lamb
dipole.)
- one direction:
This is a very simple field where the field vectors are pointing
in the same direction everywhere with the same magnitude.
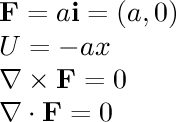
- 1/r^2 sphere:
This field is associated with gravitational attraction.
Consider the gravitational field around a planet.
Outside the planet, the field acts as if the planet were a point
mass; the field is inversely proportional to the square of the
distance from the center of the planet.
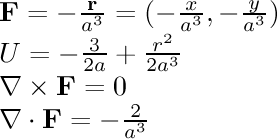
- const radial:
In this field, the particle is being pulled towards the center
with a constant force no matter where it is. I am not aware of
any real physical force that behaves like this, but if there were
one, this is what it would look like.
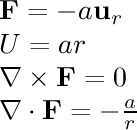
- linear radial:
In this field, the particle is being pulled towards the center
with a force proportional to its distance from the center, similar
to the force on an object attached to a spring.
This force
looks more interesting when Display: Particles (Force) is
used instead of a velocity field.
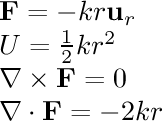
- constant to z axis:
In this field, the field vectors are pointing
towards the z axis with the same magnitude everywhere.
- constant to xy plane:
The field vectors are pointing
towards the xy plane with the same magnitude everywhere.
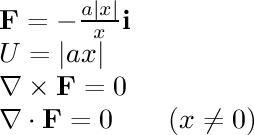
- linear to z axis:
The field vectors are pointing
towards the z axis with a force proportional to the distance
to that axis.
This force
looks more interesting when Display: Particles (Force) is
used instead of a velocity field.
- linear to xy plane:
The field vectors are pointing
towards the xy plane with a force proportional to the distance
to that plane.
This force
looks more interesting when Display: Particles (Force) is
used instead of a velocity field.
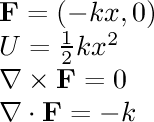
- linear to yz, xz plane:
There is a force
towards the yz plane proportional to the distance
to that plane, as well as a similar force
towards the xz plane. The relative strength of the two
forces is adjustable.
This force
looks much more interesting when Display: Particles (Force) is
used instead of a velocity field; in that case, the particles
trace out
Lissajous figures.
These are easier to see after hitting the Reset button, or when
using a small number of particles.
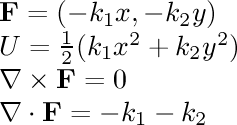 <
<
- linear to yz, xz, xy planes:
There is a force
towards the yz plane proportional to the distance
to that plane, as well as similar forces
towards the xz and xy planes. The relative strength of the three
forces is adjustable.
This force
looks much more interesting when Display: Particles (Force) is
used instead of a velocity field.
- inverse to xy plane:
There is a force
towards the yz plane inversely proportional to the distance
to that plane.
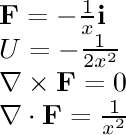
- 1/r^2 rotational:
In this field, the particle is being pulled in a circle around the
center. The speed of its motion is inversely proportional to the
square of the distance from the center.
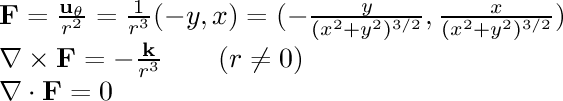
- linear rotational:
In this field, the particle is being pulled in a circle around the
center. The speed of its motion is directly proportional to the
distance from the center.
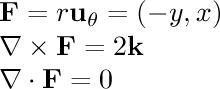
- fz=-(x^2+y^2): Here the force is
equal to (0, 0, -(x^2+y^2)). The curl of this field is the
linear rotational field.
- constant rotational:
The particle is being pulled in a circle around the
center. The speed of its motion is fixed.
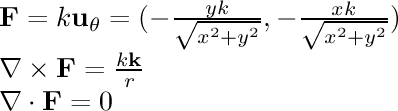
- (0,0,-r):
The curl of this field is the constant rotational field.
- helical: here the particles move in a helix.
- fx=y
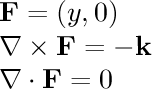
- fx=y^2
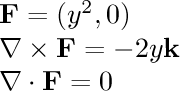
- (-yz,xz,0)

- (yz,xz,0)

- (-x,-y,2z): this is the curl of (-yz,xz,0).
- (-x,y,0): this is the curl of (yz,xz,0).
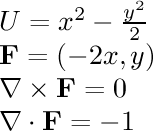
- (x-y,x+y,0)
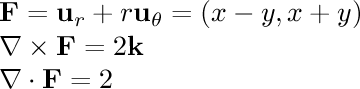
- (x-y,x+y,2z)
- Rössler attractor:
This is a strange
attractor discovered by Otto Rössler.
The parameter c (from the field equations)
is adjustable, as well as the scale in the
z direction.
- Lorenz attractor: this is another strange attractor,
discovered by Edward Lorenz. You can make
the attractor pattern larger or smaller by adjusting the scale.
- user-defined potential: this allows you to enter
an arbitrary potential function into a text box. The field vectors
will be calculated from it. A sample potential is x*x-z*z,
which is a saddle potential. Here are some other sample expressions,
to give you an idea of the input format:
x+y-z
-x^2+5.2*y
2*sin(x)+3*y
1000/(r^2)-5*z
abs(x)
exp(2*log(x+10))+sqrt(y+10)
After entering a new potential, press return so that the change
takes effect. If nothing happens, then the field may be too weak; either
increase the field strength, or multiply the field by a large constant.
If particles jump around randomly with no apparent pattern, the field
may be too strong.
Each coordinate ranges
from -10 to 10, so the edges of the box are at (±10,±10,±10).
The center of the box is the origin.
- user-defined field: this allows you to enter
an arbitrary field into text boxes (one for each coordinate).
If you try to enter some of the predefined fields (like (yz,xz,0))
into the text boxes so you can modify them, keep in mind that the
correct input format is y*z, not yz. Also the field
will not appear exactly the same, because many of the predefined
fields have a constant scaling factor that isn't reflected in the name
of the field.
The Display popup will allow you to select how the field
is displayed:
- Display: Particles (Vel.) means particles will move through
the field, with the field vectors determining their velocity.
Note that the particles are only a educational device
intended to show what the field looks like;
in real life, particles would not move in this manner.
- Display: Particles (Force) means particles will move through
the field, and the field vectors determine their acceleration.
- Display: Field Vectors shows you the field vectors at an array
of locations.
- Display: Streamlines shows you the streamlines. The
Line Density slider controls how many streamlines to draw. The
color indicates the field strength.
- Display: Equipotentials shows you equipotential surfaces.
By default slicing is turned on because the equipotentials are easier
to see that way, and you can see more than one at a time. Red means
negative potential, green means positive, gray means ground. If you
turn slicing off, you can only see one equipotential at a time;
the Potential slider allows you to determine which one to
view. If the slider is set too high or too low then the corresponding
equipotential surface may not be visible or may not exist, so just
play around with the slider a bit if you don't see anything.
The Mouse popup controls what happens when you click on the box.
If you set it to Adjust Angle or Adjust Zoom, you can
adjust the orientation or size of the 3-d view by clicking and
dragging on the box.
The Slice popup allows you to look at planar slices of the box
rather than looking at the contents of the entire box.
If the popup is set to No Slicing, you view the entire
box. Otherwise you will see the box sliced in one of three
directions. The location of the slice can be adjusted by dragging
the line running along the sides of box near the slice.
The Stopped checkbox will stop the particles.
The Reverse checkbox will reverse the direction of all the
field vectors.
The Reset button can be used to reset the positions of
all the particles to random values.
The Kick button can be used to give all the particles a
random acceleration in some direction.
This is only allowed if the particle movement is set
to "Force". It can be useful if none of the particles are moving,
or if they are all moving in the same direction.
The Field Strength slider makes the field stronger or weaker,
and also adjusts the brightness of the field vectors if you
have Display: Field Vectors selected.
The Vector Density slider controls the number of vectors present
if you have Display: Field Vectors selected.
The Number of Particles slider allows you to reduce the number
of particles, which can be useful if you want to watch the behavior of
just a few of them. Also it might speed things up if you have fewer
particles.
A few additional field-specific sliders may be present,
depending on the field you have selected.
Click here to go to the applet.


java@falstad.com
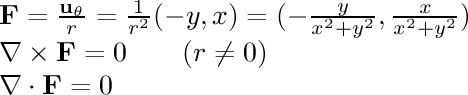
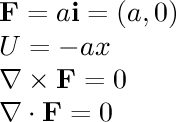
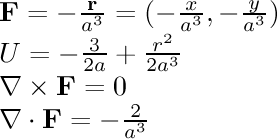
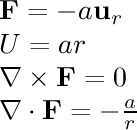
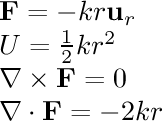
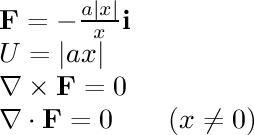
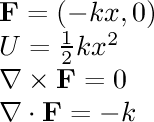
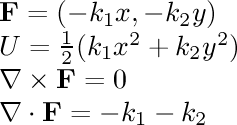 <
<